bigergm: Fit, Simulate, and Diagnose Hierarchical Exponential-Family Models for Big Networks

Cornelius Fritz, Michael Schweinberger, and David R. Hunter

Roadmap: bigergm workshop

  1. Local dependence leveraging additional structure
  2. Preparation and Background
  3. Demonstration of bigergm
  4. Application to Twitter (X): Following Network of State Legislators

Local dependence leveraging additional structure:
Non-overlapping blocks

Motivation

  • Exponential Random Graph Models (ERGMs) express the probability of observing a network as a function of network features:

\[ \mathbb{P}_{\beta}(\mathbf{x}| \mathbf{y}) = \exp\left(\beta^\top \mathbf{s}(\mathbf{x}, \mathbf{y})\right)/ c(\beta, \mathbf{y}) \] where

  • network \(\mathbf{x} = \{0,1\}^{N\times N}\)
  • \(p\) covariates \(\mathbf{y} = (y_{i,p}) \in \mathbb{R}^{N\times q}\)
  • \(\beta \in \mathbb{R}^p\) parameters
  • \(\mathbf{s}(\mathbf{x}, \mathbf{y})\) network features
  • \(c(\beta, \mathbf{y})\) normalizing constant

Exponential Random Graph Models for Big Networks

Exponential Random Graph Models for Big Networks

\[ \begin{split} \mathbb{P}_\theta(\mathbf{x} | \mathbf{y}, \mathbf{z}) = &\left[\prod_{k \neq l}^K \mathbb{P}_{B}(\mathbf{x}_{k,l} | \mathbf{y}, \mathbf{z})\right] \left[\prod_{k = 1}^K \mathbb{P}_{W}(\mathbf{x}_{k,k} | \mathbf{y},\mathbf{z}) \right] \end{split} \] where

  • \(\mathbf{x}_{k,l}\) is the submatrix of \(\mathbf{x}\) between blocks \(k\) and \(l\)
  • \(\mathbf{x}_{k,k}\) is the submatrix of \(\mathbf{x}\) within block \(k\)
  • \(\mathbf{y}\) is the covariate matrix
  • \(\mathbf{z}\) is the block structure of the network

Specification: Within-block Model

\[ \mathbb{P}_{W}(\mathbf{x}_{k,k} | \mathbf{y}, \mathbf{z}) = \exp\left(\alpha^\top \mathbf{s}_W(\mathbf{x}_{k,k}, \mathbf{y})\right)/ c_W(\alpha, \mathbf{y}, \mathbf{z}), \]

where

  • \(\mathbf{s}_W(\mathbf{x}_{k,k}, \mathbf{y})\) is a vector of network features counting, e.g., the edges within block \(k\)
  • \(\alpha\) parameter to estimate
  • \(c_W(\alpha, \mathbf{y}, \mathbf{z})\) is the normalizing constant

Degree Isolates Shared Partner

Specification: Between-block Model

\[ \mathbb{P}_{B}(\mathbf{x}_{k,l} | \mathbf{y}, \mathbf{z}) = \prod_{(i,j) \text{; } z_{ik} = 1 \text{, } z_{jl} = 1} \mathbb{P}_{\beta}( x_{i,j} \mid \mathbf{y}, \mathbf{z}), \] where \[ \mathbb{P}_{\beta}( x_{i,j} | \mathbf{y},\mathbf{z}) = (\pi_{k,l}(\beta, \mathbf{y}))^{x_{i,j}} (1 - \pi_{k,l}(\beta, \mathbf{y}))^{1 - x_{i,j}} \] e.g.

\[ \pi_{k,l}(\beta, \mathbf{y}) = \text{logit}^{-1}\left(\beta_0 + \sum_{p = 1}^P \beta_p \, \mathbb{I}\left(y_{i,p} = y_{j,p}\right) \right) \]

Specification: Between-block Model

\[ \mathbb{P}_{B}(\mathbf{x}_{k,l} | \mathbf{y}, \mathbf{z}) = \exp\left(\beta^\top \mathbf{s}_B(\mathbf{x}_{k,l}, \mathbf{y})\right)/ c_B(\beta, \mathbf{y}, \mathbf{z}), \] where \[ \mathbf{s}_B(\mathbf{x}_{k,l}, \mathbf{y}) = \left(\sum_{i<j} x_{i,j},\sum_{i<j} \mathbb{I}(y_{1,i} = y_{1,j})\, x_{i,j}, ..., \sum_{i<j} \mathbb{I}(y_{P,i} = y_{P,j})\, x_{i,j}\right) \]

Remarks:

  1. Within- and between-block models can be represented by ERGMs
  2. Between-block models do not include terms that induce dependence between connections

Estimation

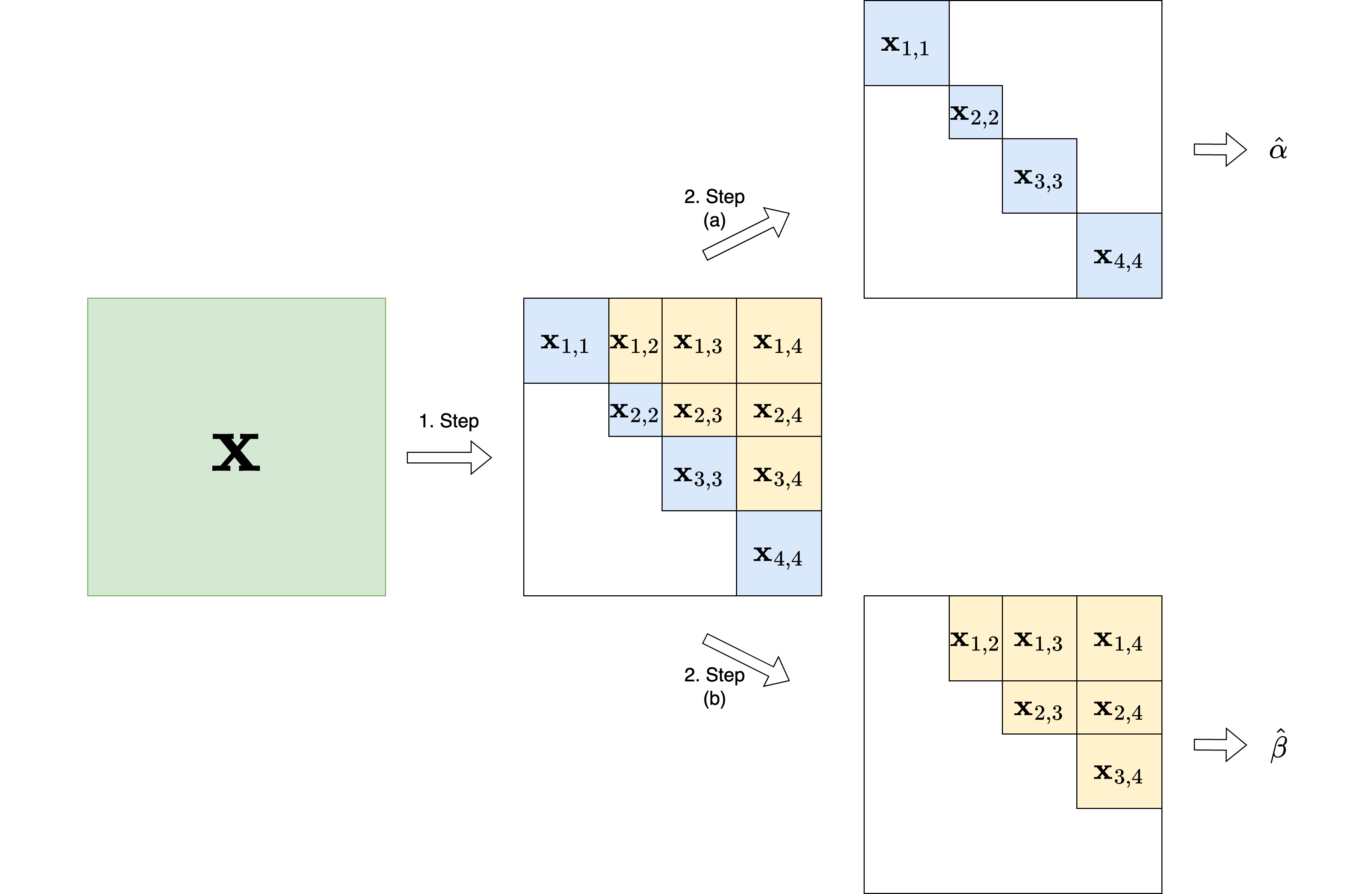
Background and Preparation

Presentation features

  1. TOC available after pressing the three stripes in the upper right corner
  2. PDF output under Tools menu
  3. Code can be copied by pressing the Copy to Clipboard button
a <- 1

The package bigergm

  • \(\mathtt{hergm}\): First package developed by Schweinberger & Luna (2018).
  • \(\mathtt{lighthergm}\): Scaling up estimation to big networks based on Babkin, Stewart, Long, & Schweinberger (2020) and Dahbura, Komatsu, Nishida, & Mele (2021)
  • \(\mathtt{bigergm}\): Extension to directed networks with a clean interface and additional features based on Fritz, Georg, Mele, & Schweinberger (2024)

Installation

  • The package can be installed in R as follows:
install.packages("bigergm", dependencies = TRUE)
  • An alternative is to install the package from GitHub:
devtools::install_github("cfritz/bigergm-tutorial", dependencies = TRUE)

bigergm: Hierarchical exponential-family random graph models for big networks

bigergm: Hierarchical exponential-family random graph models for big networks

  1. Specify
  2. Simulate
  3. Estimate
  4. Diagnose

1. Specify

Specify a ERGM with additional structure

  1. Within-block ERGM (colored blue)
  2. Between-block ERGM colored yellow)

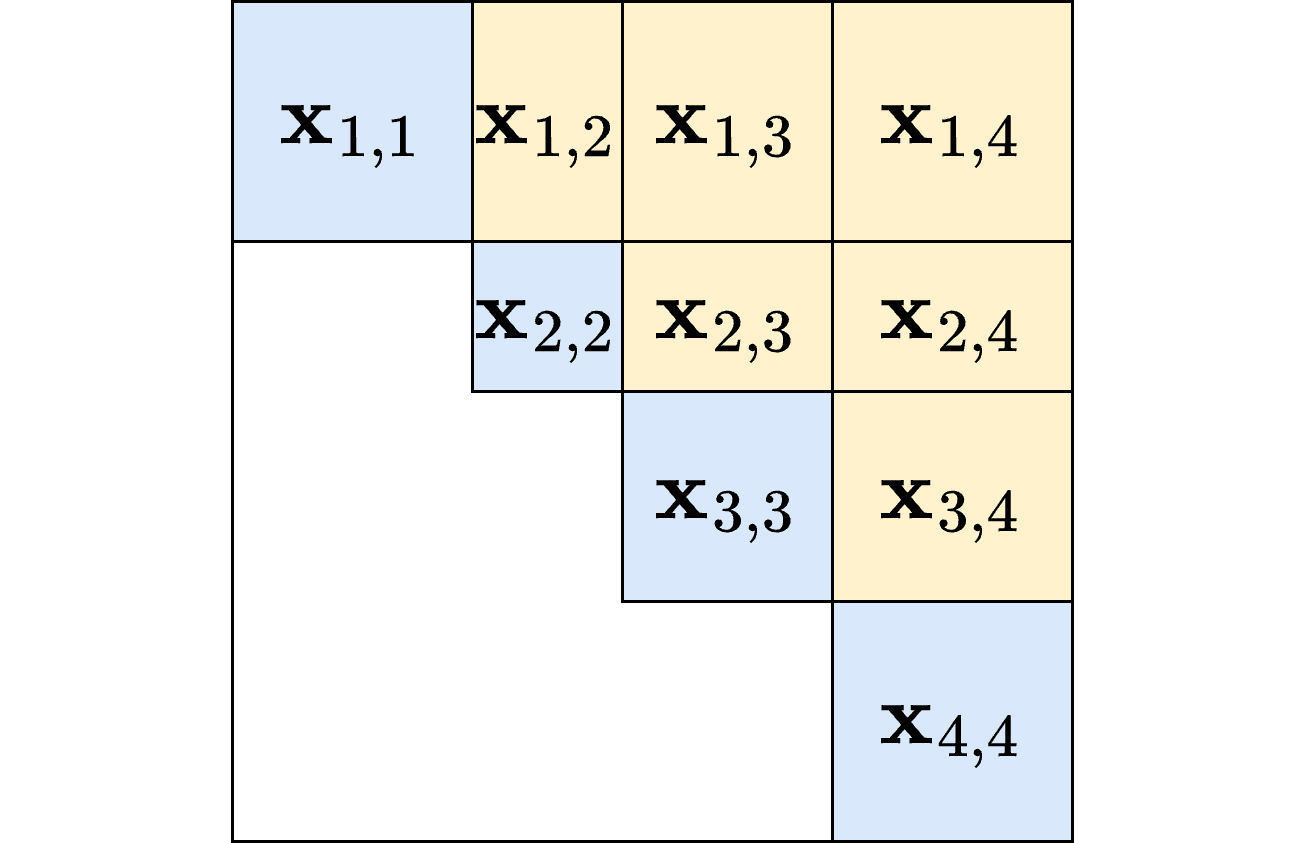
Specify a ERGM with additional structure

The block memberships saved as a vertex attribute ‘block’:

model_formula <- lhs_network ~ network_term_1 + ... + network_term_p
  1. lhs_network:
    • A network object where the simulation should be started.
    • Defines the size of the network and its directionality.
  2. network_term(s): ergmTerms specifying the network model.
    • Within-block ERGM: Dyad-independent or dyad-dependent terms
    • Between-block ERGM: Only dyad-independent terms

Example 1

model_formula <- network_tmp ~ edges   + nodematch("x") + nodematch("y")

Within-block model: \[ \mathbf{s}_W(\mathbf{x}_{k,k}, \mathbf{y}) = \left(\sum_{i<j} x_{i,j}, \sum_{i<j} \mathbb{I}(y_{1,i} = y_{1,j})\, x_{i,j}, \sum_{i<j} \mathbb{I}(y_{1,i} = y_{1,j})\, x_{i,j}\right) \] Between-block model: \[ \mathbf{s}_B(\mathbf{x}_{k,l}, \mathbf{y}) = \left(\sum_{i<j}x_{i,j}, \sum_{i<j} \mathbb{I}(y_{1,i} = y_{1,j})\, x_{i,j}, \sum_{i<j} \mathbb{I}(y_{1,i} = y_{1,j})\, x_{i,j}\right) \]

Example 2

model_formula <- network_tmp ~ edges + nodematch("x") + nodematch("y") + 
  transitiveties

Within-block model: \[ \begin{split} \mathbf{s}_W(\mathbf{x}_{k,k}, \mathbf{y}) = \Bigg(&\sum_{i<j} x_{i,j}, \sum_{i<j} \mathbb{I}(y_{1,i} = y_{1,j})\, x_{i,j}, \sum_{i<j} \mathbb{I}(y_{1,i} = y_{1,j})\, x_{i,j}, \\ &\sum_{i<j} x_{i,j}\,\mathbb{I} \Bigg(\sum_{h \neq i,j} x_{i,h}\, x_{h,j}>0 \Bigg)\Bigg) \end{split} \]

Between-block model: \[ \mathbf{s}_B(\mathbf{x}_{k,l}, \mathbf{y}) = \left(\sum_{i<j}x_{i,j}, \sum_{i<j} \mathbb{I}(y_{1,i} = y_{1,j})\, x_{i,j}, \sum_{i<j}\mathbb{I}(y_{1,i} = y_{1,j})\, x_{i,j}\right) \]

2. Simulate

Simulate

  1. Specify the base network
# Load the required packages
library(bigergm)
library(network)
# Ensure that all results are reproducible
set.seed(123)
# Specify base network (which has 200 nodes and is undirected)
network_tmp <- network::network.initialize(n = 200, directed = FALSE)
# Assign a block membership to each node 
network_tmp%v% "block" <- sample(1:4, 200, replace = TRUE)
# Assign a covariate 'x' and 'y' to each node
network_tmp%v% "x" <- sample(1:5, 200, replace = TRUE)
network_tmp%v% "y" <- sample(c("A","B","C"), 200, replace = TRUE)
  1. Specify the model formula
model_formula <- network_tmp ~ edges + nodematch("x") + nodematch("y") + transitiveties

Simulate

  1. Simulate a network from specified model
sim_net <- simulate_bigergm(
  # Model specification 
  formula = model_formula,
  # The coefficients for the between connections
  coef_between = c(-4.7,0.8, 0.4),
  # The coefficients for the within connections
  coef_within = c(-2.5,1,1,0.5),
  # Number of simulations
  nsim = 1, 
  # Control argument to guide simulation
  control_within = ergm::control.simulate.formula(MCMC.burnin = 50000, 
                                                  MCMC.interval = 10000), 
  # Ensure that all results are reproducible
  seed = 123
)

Simulate

  1. Plot simulated network
plot(sim_net, vertex.col = sim_net %v% "block")

3. Estimate

Estimate with unknown block structure

# Update the formula to refer to the simulated network 
model_formula <- update(model_formula, sim_net~.)
res <-bigergm(
  # The model you would like to estimate
  object = model_formula,
  # The number of blocks
  n_blocks =  4, 
  # The maximum number of MM steps
  n_MM_step_max = 100,
  # The tolarence for the MM algorithm
  tol_MM_step = 1e-6,
  # Indicate whether clustering should take into account nodematch on x and y
  clustering_with_features = TRUE,
  # Keep track of block memberships at each iteration
  check_block_membership = TRUE
)

Estimate with unknown block structure

summary(res)
Call:
.main()

Found 4 clusters of relative sizes: 
 0.295 0.275 0.225 0.205

Results of within-cluster estimation: 
Maximum Pseudolikelihood Results:

               Estimate Std. Error MCMC % z value Pr(>|z|)    
edges          -2.70189    0.08884      0  -30.41   <1e-04 ***
nodematch.x     0.93662    0.08120      0   11.54   <1e-04 ***
nodematch.y     0.91773    0.07333      0   12.52   <1e-04 ***
transitiveties  0.65987    0.05540      0   11.91   <1e-04 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Results of between-cluster estimation: 
 Results:

            Estimate Std. Error MCMC % z value Pr(>|z|)    
edges        -4.5848     0.1062      0 -43.184  < 1e-04 ***
nodematch.x   0.5452     0.1615      0   3.375 0.000738 ***
nodematch.y   0.1856     0.1529      0   1.214 0.224796    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
AIC: 6709.794 BIC:  6736.106

Ground truth coefficients:

  • Within-block: -2.5 (edges), 1 (nm.x), 1 (nm.y), 0.5 (tt)
  • Between-block: -4.7 (edges), 0.8 (nm.x), 0.4 (nm.y)

Estimate with unknown block structure

plot(res)

Estimate with unknown block structuree

  • Compare the estimated block structure with the true block structure by the adjusted Rand index (ARI)
ari(res$block, sim_net %v% "block")
[1] 0.9867735
  • Check the clustering step for convergence
plot(res$MM_lower_bound, type = "l", xlab = "Iteration", ylab = "Lower Bound", 
     main = "Convergence of the MM algorithm")

Estimate with known block structure

res_known <-bigergm(
  # The model you would like to estimate
  object = model_formula,
  # Specify the block structure
  blocks = sim_net %v% "block"
)
summary(res_known)
Call:
.main()

Found 4 clusters of relative sizes: 
 0.225 0.275 0.29 0.21

Results of within-cluster estimation: 
Maximum Pseudolikelihood Results:

               Estimate Std. Error MCMC % z value Pr(>|z|)    
edges          -2.67073    0.08859      0  -30.15   <1e-04 ***
nodematch.x     0.93762    0.08116      0   11.55   <1e-04 ***
nodematch.y     0.91850    0.07332      0   12.53   <1e-04 ***
transitiveties  0.63566    0.05512      0   11.53   <1e-04 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Results of between-cluster estimation: 
 Results:

            Estimate Std. Error MCMC % z value Pr(>|z|)    
edges        -4.5891     0.1061      0 -43.234  < 1e-04 ***
nodematch.x   0.5562     0.1604      0   3.468 0.000524 ***
nodematch.y   0.2138     0.1516      0   1.410 0.158430    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
AIC: 6726.304 BIC:  6752.603

3. Diagnose

Diagnose

  • Check if simulations from the estimated model match the observed network
  • Function calculates degree, edgewise shared partner, and geodesic distance statistics
tmp <- gof(res_known, 
    # Control arguments for within-block simulations
    control_within = ergm::control.simulate.formula(MCMC.burnin = 50000, 
                                                    MCMC.interval = 10000), 
    # How many simulations should be performed?
    nsim = 100,
    # Either 'full' or 'within' to say if gof should be based on only 
    # within-connections or all
    type = "full",
    # Ensure that all results are reproducible
    seed = 123,
    # Should the simulation start from the observed network?
    start_from_observed = TRUE, 
    # Should all geodesic distances be computed for the simulated networks?
    compute_geodesic_distance = TRUE)

Diagnose

par(mfrow = c(2,2))
plot(tmp)

Application to Twitter (X):
Following Network of State Legislators

Data: Twitter (X) network of U.S. state legislators

We are indebted Bruce Desmarais for sharing the Twitter (X) data and allowing us to include them in the package:

  • Gopal, Kim, Nakka, Boehmke, Harden, Desmarais. The National Network of U.S. State Legislators on Twitter. Political Science Research & Methods, Forthcoming.

  • Kim, Nakka, Gopal, Desmarais, Mancinelli, Harden, Ko, and Boehmke (2022). Attention to the COVID-19 pandemic on Twitter: Partisan differences among U.S. state legislators. Legislative Studies Quarterly 47, 1023–1041.

Data: Twitter (X) network of U.S. state legislators

data("state_twitter")
state_twitter
 Network attributes:
  vertices = 2191 
  directed = TRUE 
  hyper = FALSE 
  loops = FALSE 
  multiple = FALSE 
  bipartite = FALSE 
  total edges= 33321 
    missing edges= 0 
    non-missing edges= 33321 

 Vertex attribute names: 
    gender party race state vertex.names 

 Edge attribute names not shown

Data: Twitter (X) network of U.S. state legislators

library(ggnet)
library(GGally)
# Ensure that all results are reproducible
set.seed(123)
ggnet2(state_twitter,  size = 1, color = "state", edge.alpha = 0.1) + 
  guides(color = "none") + 
  scale_colour_viridis_d()

1. Specify

  • Issue with blocks of different size: Parameters of within-block model may change between blocks
  • Solution based on ergm.multi: Size-dependent parametrizations
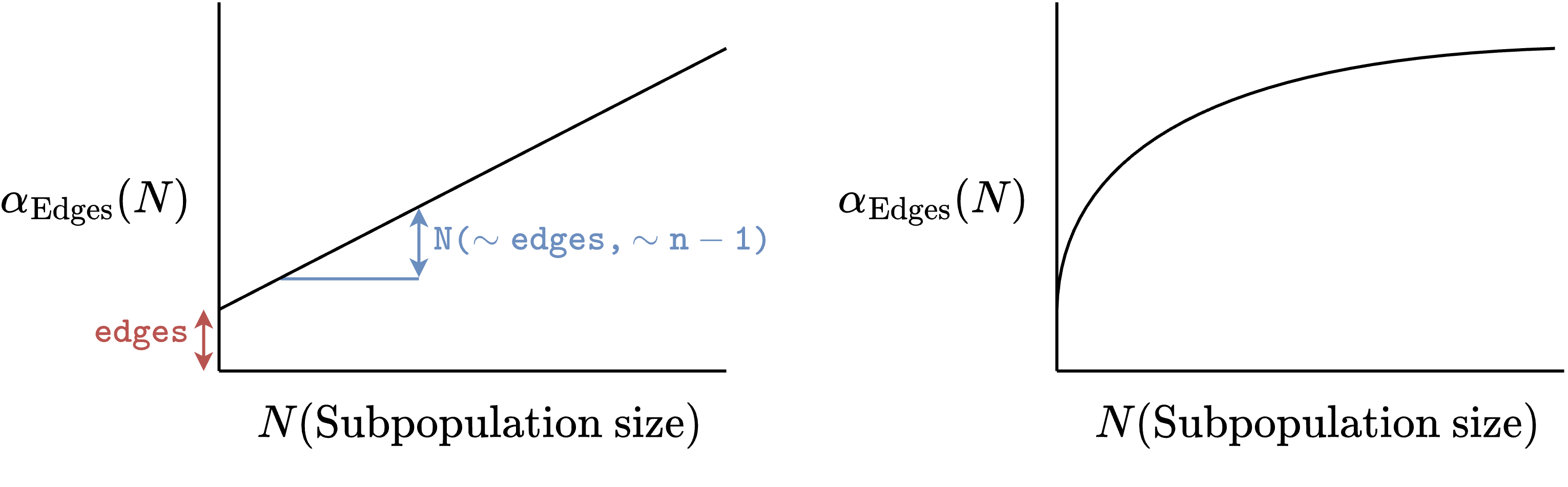
model_formula <- state_twitter ~  edges + N(~edges,~n-1) 
model_formula <- state_twitter ~  edges + N(~edges,~log(n)-1)

Exercise 1: Specification

  • Specify a HERGM for the Twitter (X) network of U.S. state legislators with the following terms:
    • Homophily based on party affiliation, race, and gender with nodematch statistic
    • Size-dependent parametrizations of the edge term
Solution 
formula_tmp <- state_twitter ~  edges + nodematch("party") + 
  nodematch("race") + nodematch("gender") + N(~edges,~log(n)-1)

Exercise 2: Estimation

  • Estimate the HERGM with the bigergm function assuming there are 50 blocks (use the covariate information for the first step)
    • Check if different initialization methods lead to different results (see help(bigergm) for guidance on availablity of different initialization methods).
    • Compare the estimated blocks with the state each legislator serves for with the adjusted Rand index (ARI).
Hint 1 
# clustering_with_features, n_blocks, initialization
help(bigergm)
Hint 2 
help(ari)
help(attribute.methods)
state_twitter%v%"state"

Exercise 2: Estimation

  • Estimate the HERGM with the bigergm function assuming there are 50 blocks (use the covariate information for the first step)
    • Check if different initialization methods lead to different results (see help(bigergm) for guidance on availablity of different initialization methods).
    • Compare the estimated blocks with the state each legislator serves for with the adjusted Rand index (ARI).
Solution 1 
twitter_tmp <- bigergm(
  object = formula_tmp,
  # Perform parameter estimation after the block recovery step
  clustering_with_features = TRUE,
  # How many blocks should be estimated?
  n_blocks = 50, 
  # Set algorithm for initialization 
  initialization = "walktrap")
Solution 2 
summary(twitter_tmp)
ari(twitter_tmp$block,state_twitter%v%"state")

Exercise 3: Simulation

  • Simulate 10 networks from the estimated model and plot the number of edges in the within- and between-block networks
Hint 
help(simulate)
help(simulate_bigergm)
Solution 
twitter_sim <- simulate(twitter_tmp, output = "stats", nsim = 10,
                        control_within = control.simulate.formula(MCMC.interval = 20000))
plot(twitter_sim$within_network$edges,
     xlab = "Index", ylab = "Within-block Edges", type = "l")
plot(twitter_sim$between_network$edges,
     xlab = "Index", ylab = "Within-block Edges", type = "l")

1. Specify

  • Issue with blocks of different size: Parameters of the within-block model might change between blocks
  • Solution based on ergm.multi: Size-dependent parametrizations!
model_formula <- state_twitter ~  edges + nodematch("party") +   
   nodematch("race") + nodematch("gender") + N(~transitiveties,~log(n)) + 
   N(~mutual,~log(n)) + N(~edges,~log(n)-1)

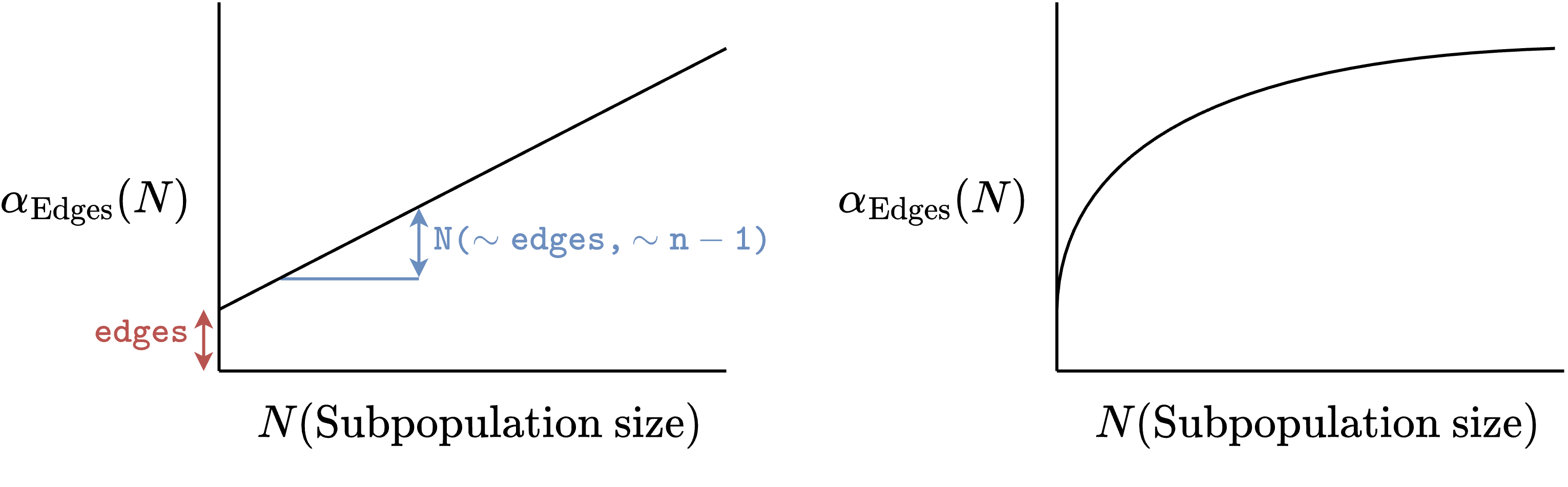
2. Estimate

  • Support for parallel computation and ML estimation for within-block model
twitter_res <- bigergm(
  object = model_formula,
  # The number of blocks
  n_MM_step_max = 1000,tol_MM_step = 0.0001,
  # The maximum number of MM steps 
  estimate_parameters = TRUE,
  # Perform parameter estimation after the block recovery step
  clustering_with_features = TRUE,
  # Indicate wether clustering should take into account 
  # nodematch on characteristics
  check_block_membership = TRUE, 
  # How many blocks should be estimated?
  n_blocks = 50,
  # Which estimation for the within-block model should be used?
  method_within = "MLE",
  # Control arguments for within-block simulations
  control_within = control.ergm(parallel=5, parallel.type="PSOCK", 
                                MCMC.burnin = 10000, 
                                MCMC.interval = 20000))

2. Estimate

  • Homophily based on party affiliation
  • Strong reciprocity, decreasing with network size
  • Strong transitivity, decreasing with network size
summary(twitter_res)
Call:
.main()

Found 50 clusters of relative sizes: 
 0.02418987 0.02008215 0.02784117 0.01780009 0.0109539 0.03651301 0.02647193 0.01643085 0.01916933 0.03833866 0.03012323 0.03194888 0.005933364 0.01688727 0.005476951 0.01186673 0.01962574 0.01141031 0.03423094 0.04792332 0.02008215 0.04198996 0.009128252 0.03103606 0.01414879 0.007302602 0.01506162 0.02555911 0.0182565 0.007302602 0.01916933 0.01186673 0.02555911 0.02510269 0.02921041 0.007302602 0.02099498 0.01551803 0.005476951 0.01141031 0.03423094 0.02555911 0.02373346 0.04518485 0.01597444 0.007302602 0.006389776 0.009128252 0.007302602 0.01049749

Results of within-cluster estimation: 
Monte Carlo Maximum Likelihood Results:

                         Estimate Std. Error MCMC % z value Pr(>|z|)    
edges                    -5.43754    0.28367      0 -19.169   <1e-04 ***
nodematch.party           0.94633    0.01371      0  69.034   <1e-04 ***
nodematch.race           -0.09171    0.01188      0  -7.720   <1e-04 ***
nodematch.gender          0.04617    0.01155      0   3.999   <1e-04 ***
N(1)~transitiveties       2.06586    0.24291      0   8.505   <1e-04 ***
N(log(n))~transitiveties -0.42498    0.06314      0  -6.731   <1e-04 ***
N(1)~mutual               3.42629    0.23246      0  14.739   <1e-04 ***
N(log(n))~mutual         -0.29690    0.05560      0  -5.340   <1e-04 ***
N(log(n))~edges           0.62174    0.07280      0   8.540   <1e-04 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Results of between-cluster estimation: 
 Results:

                 Estimate Std. Error MCMC %  z value Pr(>|z|)    
edges            -8.03344    0.04456      0 -180.263   <1e-04 ***
nodematch.party   1.57107    0.04033      0   38.956   <1e-04 ***
nodematch.race   -0.16491    0.03039      0   -5.427   <1e-04 ***
nodematch.gender  0.19144    0.03030      0    6.319   <1e-04 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
AIC: 184693.6 BIC:  184784.2

2. Estimate

  • Exploit that est_within is an ergm object
  • Check if the MCMC chains used for estimation have converged
par(mfrow = c(2,2))
mcmc.diagnostics(twitter_res$est_within,which = "plots")


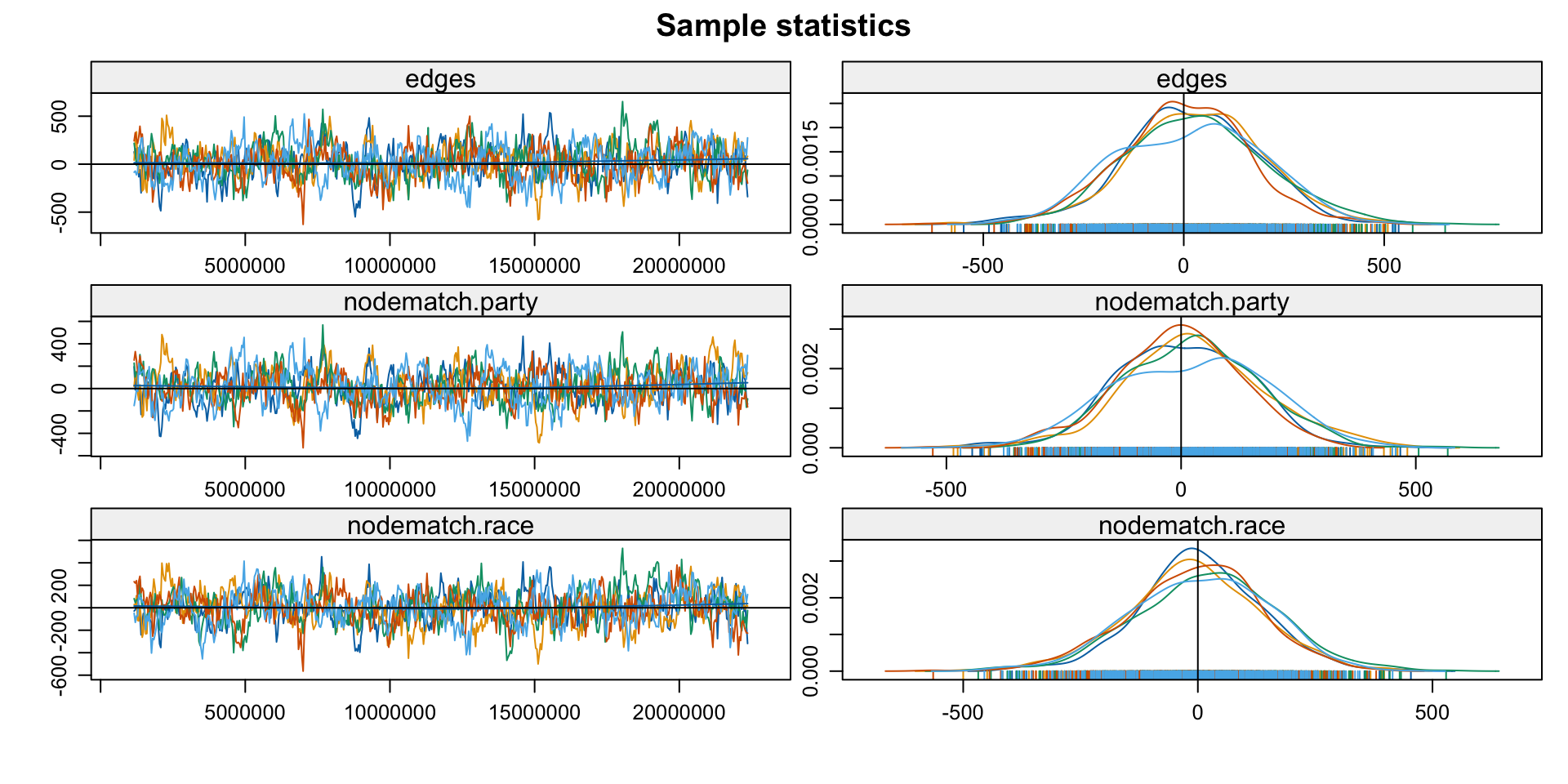
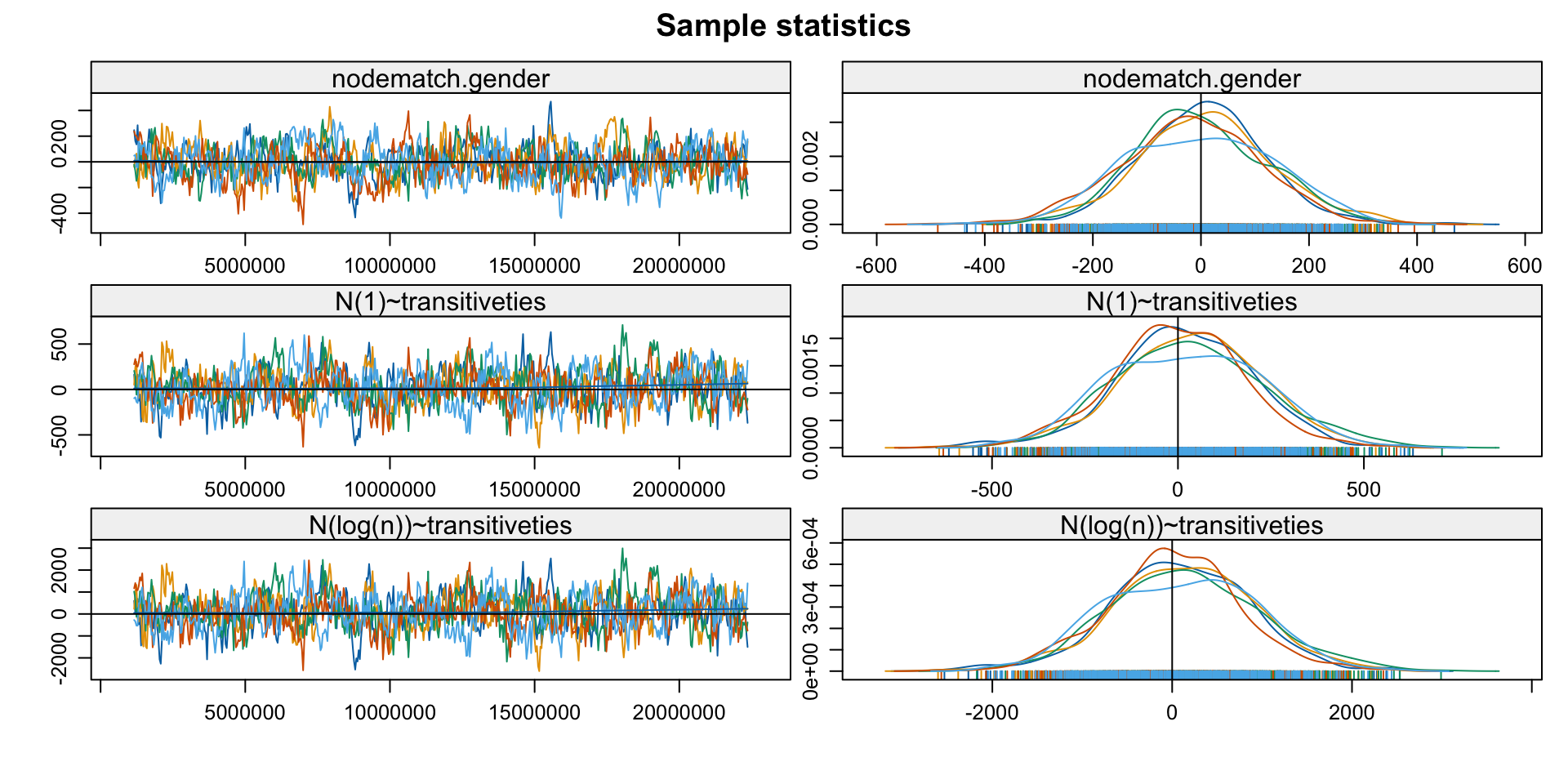
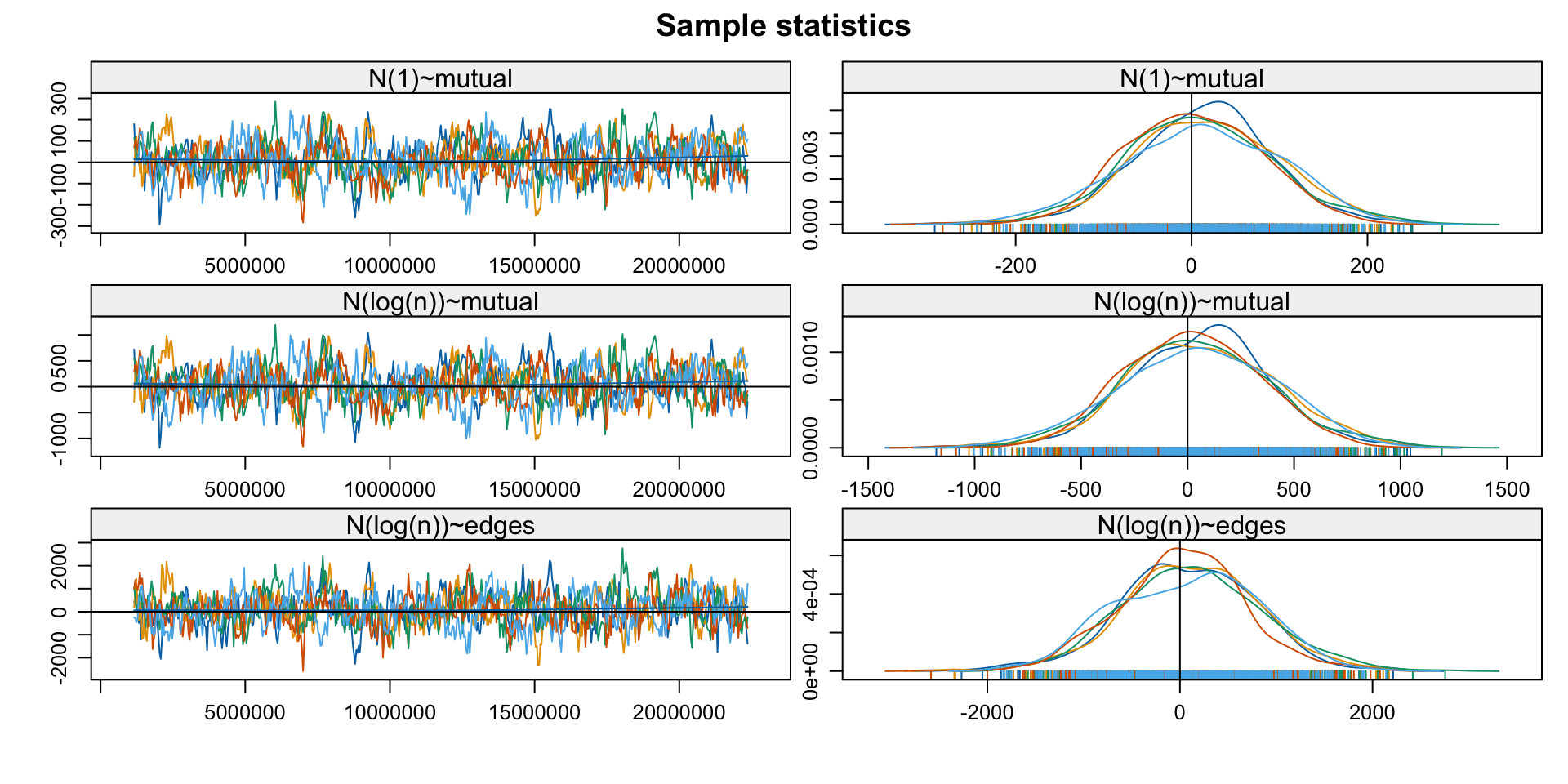
Note: MCMC diagnostics shown here are from the last round of
  simulation, prior to computation of final parameter estimates.
  Because the final estimates are refinements of those used for this
  simulation run, these diagnostics may understate model performance.
  To directly assess the performance of the final model on in-model
  statistics, please use the GOF command: gof(ergmFitObject,
  GOF=~model).

3. Diagnose: GoF

sim_networks <- simulate(twitter_res, nsim = 100, seed = 2, 
                         control_within = control.simulate.formula(parallel=5,
                                                                   parallel.type="PSOCK", 
                                                                   MCMC.burnin = 20000, 
                                                                   MCMC.interval = 30000))
Code 
simulated <-  mapply(FUN = function(x) {
  tmp_x <- get_within_networks(x, x%v%"block")
  summary(tmp_x ~transitiveties + triangle + edges + mutual)
}, x = sim_networks,
SIMPLIFY = FALSE)
simulated <- do.call(rbind, simulated)
state_twitter_block <- get_within_networks(state_twitter, twitter_res$block)
observed_statistics <- summary(state_twitter_block ~ transitiveties + triangle + edges + mutual)
plot(density(simulated[,1]), xlab = "Transitivities", ylab = "Density", main = "")
abline(v = observed_statistics[1], col = "red")

3. Diagnose: GoF

# Assess fit
twitter_gof <- gof(twitter_res, 
                   # How many simulations should be performed?
                   n_sim = 100, 
                   # Ensure that all results are reproducible
                   seed = 2, 
                   # Either 'full' or 'within' to say if gof should be based on only 
                   # within-connections or all
                   type = "within", 
                   # Should the geodesic distance be computed?
                   compute_geodesic_distance = TRUE,
                   # Control arguments for within-block simulations
                   control_within = control.simulate.formula(
                                                     MCMC.burnin = 10000, 
                                                     MCMC.interval = 30000))

3. Diagnose: GoF

  • Plot the goodness-of-fit statistics
par(mfrow = c(1,2))
plot(twitter_gof)

Conclusion and Outlook

  • bigergm is a powerful tool for estimating, simulating, and diagnosing HERGMs for big networks
  • Package is under active development:
    • Degree-correction
    • Overlapping blocks
    • Bipartite networks
    • More efficient estimation algorithms
  • Feedback and contributions are welcome!

Literature

Babkin, S., Stewart, J., Long, X., & Schweinberger, M. (2020). Large-scale estimation of random graph models with local dependence. Computational Statistics & Data Analysis, 152, 107029.
Dahbura, J. N. M., Komatsu, S., Nishida, T., & Mele, A. (2021). A Structural Model of Business Card Exchange Networks. Working Paper. Available at https://arxiv.org/abs/2105.12704.
Fritz, C., Georg, C.-P., Mele, A., & Schweinberger, M. (2024). A strategic model of software dependency networks. Working Paper. Available at https://arxiv.org/abs/2402.13375.
Schweinberger, M., & Luna, P. (2018). hergm: Hierarchical Exponential-Family Random Graph Models. Journal of Statistical Software, 85(1), 1–39.